reformuler

reformuler [ r(ə)fɔrmyle ] v. tr. <conjug. : 1>

• 1954 ; de re- et formuler

♦ Formuler à nouveau, généralement de façon plus claire. Reformuler sa demande.

● reformuler verbe transitif Formuler de nouveau et d'une manière plus correcte.

⇒REFORMULER, verbe trans.

Formuler, exprimer de nouveau, autrement. Enrichie et précisée dans les luttes sociales, reformulée au contact de leur expérience, cette idée est propre à élargir les conceptualisations systématiques (PERROUX, Écon. XX^e s., 1964, p. 592). Reformulation des discours scientifiques et techniques dans diverses situations: celles de l'enseignement, de la traduction, des échanges conversationnels au laboratoire, de la « vulgarisation ». Autant de lieux et de motifs pour reformuler un discours second, sans que s'efface, au passage, le label « scientifique et technique » (Lang. fr., 1984, n ° 64, av.-pr.).

— Empl. pronom. L'enseignement du christianisme médiéval sur l'intérêt trouve au XX^e siècle des confirmations assez inattendues, en même temps que des occasions pressantes de se reformuler en se rajeunissant (PERROUX, Écon. XX^e s., 1964, p. 370).

Prononc.:[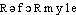], (il) reformule [-myl]. Étymol. et Hist. 1954 part. passé (AMADOU, Parapsychol., p. 148). Dér. de formuler; préf. re-.

DÉR. Reformulation, subst. fém. Nouvelle formulation qui reproduit autrement ce qui a déjà été exprimé. Au morcellement de la personnalité entre le ça, le moi, le surmoi et l'idéal du moi, s'est substitué, dans une reformulation récente de la psychanalyse orthodoxe, depuis les travaux de Reik, le point de vue de l'ego et de sa structure (Traité sociol., 1968, p. 406). V. supra ex. de Lang. fr. — [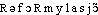]. — 1^re attest. 1968 id.; de reformuler, suff. -(a)tion.

BBG. — QUEM. DDL t. 31.

reformuler [ʀ(ə)fɔʀmyle] v. tr.

ÉTYM. XX^e; de re-, et formuler.

❖

♦ Didact. Donner une nouvelle formulation à.

Encyclopédie Universelle. 2012.